video2 video3COVID-19: Matemática…¿Estás aquí?. El Teorema del Umbral – Investigación de docentes de la Universidad Nacional del Comahue. #UNCo – #UNComa. Autores/as: Hugo Aimar, Raquel Crescimbeni, Nicolas Silva Nash, Luis Nowak, Alejandra Perini
A la matemática le cabe el “arduo honor” de un ascetismo ideológico, que le ha permitido
desarrollar modelos estocásticos para las fluctuaciones de las cotizaciones en las Bolsas
que comparten con los inicios del cálculo de probabilidades, hace siglos, sus aspiraciones
predictivas de lo aleatorio. No pocas veces en pos de beneficios financieros: la timba.
No hace falta hacer una lista de teoremas con los que otros valores humanos, que son más
esenciales que la renta financiera, se han visto beneficiados. Basta nombrar, pensando en
la salud humana, la transformada de Radon que es la base teórica de la tomografía
computada. Entre tantos otros.
Como nos dice Pablo Neruda “hoy que los pistoleros se pasean con la cultura occidental
en brazos” y con los golpes en las cacerolas para tratar de sostener a toda costa la
estructura económica y financiera, que es la mayor responsable de la crisis asociada a
COVID-19 por la mercantilización de la salud y la consecuente destrucción mundial de las
estructuras de salud pública, vale la pena preguntarnos Matemática…¿estás aquí?.
Y no sólo la salud pública es la víctima de estos procesos de achicamiento sistemático, sino
lo público como categoría de la estructura social. En particular el sistema científico en
nuestro país ha sufrido en este último tiempo un duro golpe y necesita ser fortalecido.
Todos los avances tecnológicos y las respuestas a problemas, como el que nos ocupa, se
basan en fuertes y sólidos conceptos y resultados de la investigación científica. No se
pueden desarrollar aplicaciones sin un desarrollo de la ciencia básica y es vital
retroalimentar de manera virtuosa ese vínculo.
Por cierto que toda la información gráfica circulante que nos ilustra casi siempre, y nos
abruma a veces, relativa a la evolución de la pandemia en diferentes países y la frenética
búsqueda de relaciones entre las dinámicas observadas y causalidades ocultas están
escritas en lenguaje matemático. Pero la matemática como actividad humana se
manifiesta no sólo a través de su lenguaje sino, sobre todo, a través del hallazgo
demostrado de relaciones internas en un modelo, que son invisibles a priori. Y muchas
veces insospechadas. Estos hallazgos son los Teoremas.
Y entre ellos, hay algunos que se destacan por su versatilidad para adaptarse a diversos
contextos. Por su impacto en el desarrollo de ricas teorías matemáticas y su utilidad en
diversas aplicaciones. Son esas gemas que nos brinda la matemática y este artículo tiene
2
por protagonista a una de ellas: el Teorema del Umbral. Resultado de la Teoría
Matemática de las Epidemias publicado en el año 1927 en un trabajo de Kermack y
McKendrick [KM].
La simplicidad en la formulación de este teorema es lo que nos permite entender porqué
son importantes las medidas de aislación social que estamos cursando.
Hay dos números involucrados en el Teorema del Umbral, N y R0.
El primero N, es el número de pobladores de la comunidad en la que está produciéndose
la epidemia. Suponemos aquí que las fronteras están cerradas y no hay ingresos ni egresos
de pobladores durante el periodo de evolución de la epidemia.
El segundo, R0 (el número básico de reproducción), contiene toda la información relevante
al desarrollo del virus en la comunidad particular a la que infecta. Para entenderlo
consideremos dos situaciones de desarrollo de la epidemia en la comunidad que estamos
intentado controlar: 1) la cantidad de infectados se duplica en una semana; 2) la cantidad
de infectados se triplica en 14 días. El escenario más favorable de los dos para la salud
pública es el segundo porque, mientras que en el caso 1) la cantidad de infectados se
multiplica por dos en una semana, en el caso 2) se multiplica por 1,5 en una semana. Ese
factor es el número R0. Y es claro porqué resulta importante que, aún siendo una fracción
mayor que la unidad, R0 sea lo más cercano a uno posible. Efectivamente cuando R0 es
más cercano a uno la epidemia se desacelera.
Estas consideraciones son muy intuitivas y razonables. Pero el llamado Teorema del
Umbral provee una información sobre el máximo número de infectados, que llamamos U,
durante la epidemia en términos de esos dos números, N y R0.
TEOREMA DEL UMBRAL: El número de infectados crece hasta un valor máximo que está
dado por
? = ? –?
??
Esencialmente, en este caso del COVID-19 que estamos viviendo actualmente, cuando se
nos dice que las medidas que se toman son para aplanar la curva, se lo hace en base al
Teorema del Umbral que acabamos de enunciar. Veamos entonces cómo se interpreta
este resultado y mostremos, brevemente, gráficamente y sin entrar en tecnicismos, la
manera en que nos está ayudando a tomar decisiones.
3
Para un valor fijo de R0, el siguiente video muestra como es el comportamiento de las
curvas que indican las cantidades de Infectados (curva roja), de susceptibles de ser
infectados (curva azul) y los recuperados o fallecidos (curva verde) en función del
transcurrir del tiempo.
VIDEO1
Centremos la mirada en la curva roja de los infectados en el video anterior. Veamos, con
otro esquema de representación, como el número de infectados cambia si cambia el valor
de reproducción inicial R0.
Por ejemplo, si tomamos un valor de R0=3 y una ventana temporal de 7 días en la cual en
promedio una persona infectada contagia a las otras, tendremos que un recién infectado
contagia a tres personas a los 7 días de haberse infectado, en promedio. Pero una vez que
el proceso ha comenzado esta transmisión del virus comienza a replicarse cada 7 días. Es
decir, cada nuevo infectado contagia a otros tres y así siguiendo. Notemos que si variamos
el parámetro R0 la dinámica se puede desacelerar o acelerar. Por ejemplo cambiando el
número básico de reproducción a R0 = 2 la dinámica se desacelera.
En el siguiente video podemos visualizar como el cambio del valor de reproducción inicial
R0 modifica el gráfico de las tres curvas. Notar que la visualización que se presenta aquí
muestra el comportamiento a medida que bajamos el número básico de reproducción.
VIDEO2
Dos consecuencias de la disminución de R0 son visibles en el video anterior. La primera es
la disminución del máximo de cada curva roja. La segunda es el desplazamiento del
máximo de la curva roja hacia la derecha, esto es hacia el futuro.
Un hecho crucial asociado a la implementación de adecuadas medidas sanitarias que
permitan desconcentrar el uso de los recursos hospitalarios y simultáneamente su
postergación, es que R0 depende también de las propiedades de aislación o conductividad
de la población en la que el virus prospera. Como en el caso de la electricidad, hay
sustancias conductoras, como el cobre. Hay sustancias aislantes, como los plásticos que
envuelven los cables. Y en este caso ser aislantes y no conductores depende del
comportamiento de la sociedad. De nosotros. ¿Cómo podemos tener el control de R0? Por
un lado tomando recaudos de lavar las manos regularmente con agua y jabón y mantener
una distancia prudente entre personas (para el caso del Coronavirus COVID-19 es de entre
un metro y medio y dos metros). Este comportamiento social puede hacer que baje la
probabilidad de contacto. Pero cuando aún con eso el crecimiento de casos es muy
pronunciado debe recurrirse a otras medidas más drásticas como el aislamiento.
4
Este comportamiento social puede hacer que baje la probabilidad de contacto. Los dos
siguientes videos, extraídos de una publicación en la red social Twitter y de un artículo del
Washington Post, muestran mediante simulaciones las ventajas que provoca tomar
medidas de aislamiento ante la propagación del virus.
I explain what level 2 of NZ's #Covid_19 Alert System is in my latest @TheSpinoffTV piece. In her briefing @jacindaardern listed what we all SHOULD do now. I need you to understand that you MUST do them otherwise we'll be at level 4 before we know it. https://t.co/xQSJo9coKN pic.twitter.com/rkUazZhao5
— Dr Siouxsie Wiles (@SiouxsieW) March 21, 2020
https://drive.google.com/file/d/1b0d8W6JwdXmyCLEC1Vbkafs2EEj_k7OA/view?usp=dr
ive_web
Si restringimos la circulación estamos bajando el valor R0 y logramos tener un control de la
evolución de la epidemia que nos permita por ejemplo saber si el sistema de salud podrá
soportar la demanda de infectados que necesitarán atención médica y eventualmente
internación. Según datos oficiales y la experiencia en otras partes del mundo, se estima
que para el caso del Coronavirus COVID-19 el 20% de los infectados requerirán internación
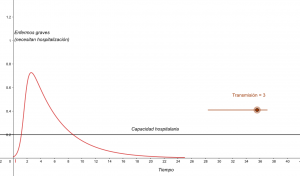
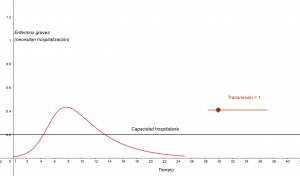
por enfermarse de manera grave o muy grave. Con estos datos, vemos, en la siguiente
simulación y gráficos, que al reducir el valor de R0=3 a R0=1 la situación cambia
radicalmente. No sólo se gana tiempo hasta alcanzar el pico máximo de infectados, sino
también se reduce notablemente la cantidad de personas que requieren internación
simultáneamente, dando así oportunidad al sistema de salud de tener una mejor reacción
de respuesta al estrés que será sometido. Aquí en el gráfico la recta de color negro indica
un número hipotético de internados que un sistema de salud puede atender según sus
capacidades y la curva roja representa sólo a la proporción de infectados que requerirán
internación.
Finalmente, para concluir y dar respuesta a Matemática,…¿estás aquí?… podemos decir
que sí. La matemática en su universalidad puede ser vista como una de las bellas artes,
como lo propone P. Amster en [A], y, claro que hemos parafraseado a A. Paenza [P],
porque ésta es una prueba más de su ubicuidad. Y aquí ha venido a decirnos, con un
Teorema de 1927, que está en nosotros como sociedad controlar la pandemia achicando
el número básico de reproducción R0. Cuarentena, aislación social, distancia, higiene y tal
vez tengamos en poco tiempo indicaciones nacionales e internacionales de usar más
cobertores faciales como máscaras o barbijos.
5
[KM] Una contribución a la teoría matemática de epidemias. W. Kermack y A. McKendrick.
Proc. Roy. Soc. A. 700-721 (1927).
[A] La matemática como una de las bellas artes. Pablo Amster. Siglo XXI editores (2008).
[P] Matemática, ¿estás ahí?. Adrian Paenza. Siglo XXI editores (2005).
A IMAL-CONICET-UNL.
B IITCI-CONICET. Dpto. de Matemática-FaEA-UNCo.
C Estudiante de Lic. en Mat. Dpto. de Matemática-FaEA-UNCo.



